Exo 6
Soit
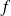la fonction définie par :
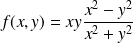si
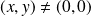, et :
.
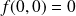Question
La fonction
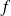est-elle continue sur
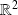? de classe
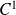? de classe
?
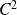A chaque étape, séparez l'étude globale sur
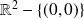et l'étude locale en
.
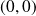La fonction est de classe
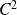sur
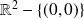par opérations sur des fonctions de classe
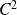(elle est même de classe
).
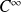Il reste à faire l'étude en
.
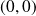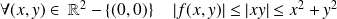. Donc :
.
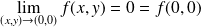Donc la fonction
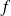est continue en
.
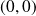Conclusion : La fonction
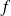est continue sur
.
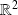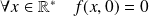, donc :
.
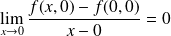Donc en
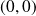, la fonction
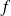admet une dérivée partielle par rapport à
:
.
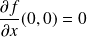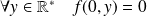, donc :
.
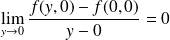Donc en
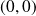, la fonction
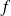admet une dérivée partielle par rapport à
:
.
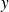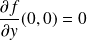Or les dérivées partielles d'ordre
sur
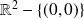sont :
. 
.
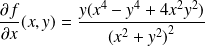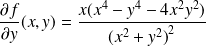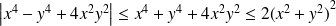, donc :
.
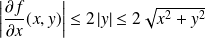Et :
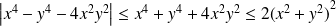, donc :
.
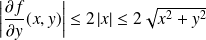Donc :
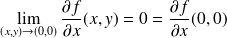, et :
.
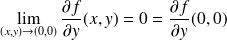Donc les dérivées partielles d'ordre
de la fonction
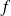sont continues en
.
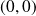Conclusion : La fonction
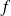est de classe
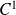sur
.
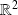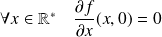, donc :
.
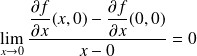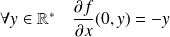, donc :
.
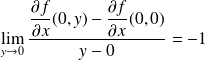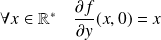, donc :
.
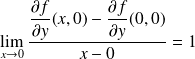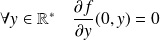, donc :
.
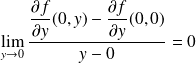Donc en
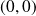, la fonction
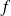admet des dérivées partielles d'ordre
:
. 
. 
. 
.
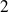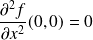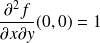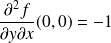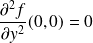On remarque que :
.
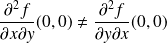Conclusion : La fonction
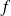est de classe
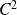sur
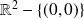, mais pas sur
.
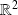