Exo 4
Soit
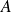une matrice de
.
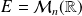Question
Démontrer que l'application
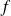qui à toute matrice
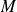de
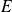associe la matrice
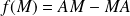est un endomorphisme de
.
Montrer que l'application
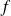est linéaire.
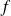est une application de
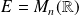dans lui-même. Montrons qu'elle est linéaire.
Soit
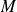et
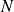deux matrices de
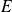, et
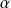un réel.
.
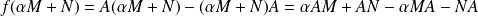Donc :
.
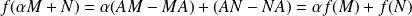Donc l'application
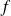est linéaire.
Conclusion : L'application
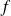est un endomorphisme de
.
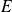Question
Montrer que les matrices
,
,
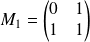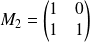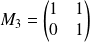et
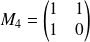forment une base
de
.
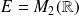Il suffit de démontrer que la famille est libre.
Montrons que la famille
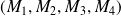est libre.
Soit
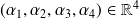tel que :
.
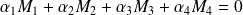Donc :
.
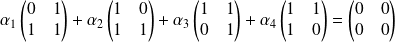Donc :
.
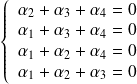En additionnant les lignes, on obtient
.
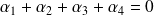Donc :
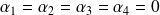. Donc la famille
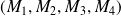est libre.
C'est une famille libre de
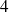vecteurs dans l'espace vectoriel
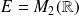qui est de dimension
.
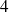Conclusion : La famille
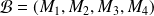est une base de
.
Question
Déterminer les coordonnées d'une matrice
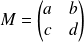dans la base
.
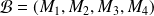si et seulement si :
.
En additionnant les lignes, on obtient :
.
Conclusion : Les coordonnées de
dans la base
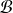sont
.
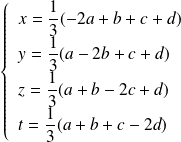Question
On suppose que
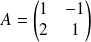et
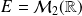. Déterminer la matrice de
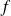dans la base
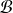de
.
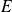Exprimez les images des vecteurs de la base
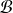de
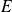dans la base
.
.
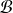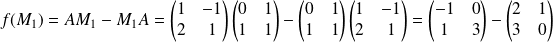Donc
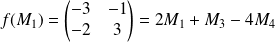d'après la deuxième question.
.
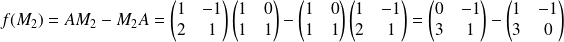Donc :
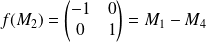d'après la deuxième question.
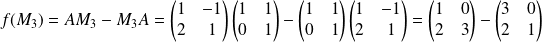
Donc :
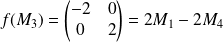d'après la deuxième question.
.
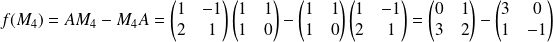Donc :
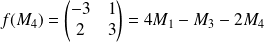d'après la deuxième question.
Conclusion : La matrice de
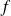dans la base
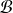est
.
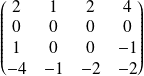