Exemple
Exemple :
Soit
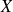 une variable aléatoire de densité
une variable aléatoire de densité
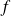 définie par :
définie par :
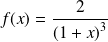 si
si
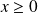 et
et
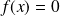 sinon.
sinon.
On rappelle que son espérance est
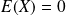 .
.
La variable
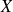 a-t-elle une variance ?
a-t-elle une variance ?
Sous réserve d'existence, l'espérance de
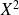 est :
est :
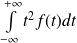 .
.
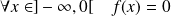 , donc
, donc
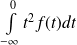 est convergente et
est convergente et
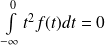 .
.
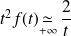 , donc l'intégrale
, donc l'intégrale
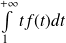 est de même nature que
est de même nature que
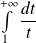 , donc divergente.
, donc divergente.
Donc
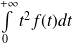 est divergente et donc
est divergente et donc
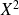 n'a pas d'espérance.
n'a pas d'espérance.
Conclusion :
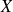 n'a pas de variance.
n'a pas de variance.
