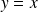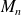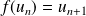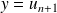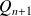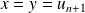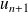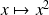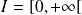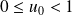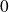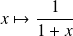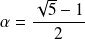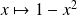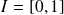Complément sur les suites récurrentes
Soit
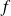une fonction continue définie sur un intervalle
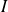de
.
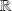Soit
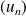la suite définie par son premier terme
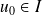et la relation :
.
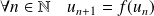Existence
Pour que la suite soit bien définie, il faut pouvoir calculer
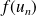pour tout entier
.
Pour cela, il suffit que la fonction
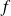soit définie sur un intervalle
de
tel que :
.
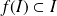Si
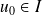, une récurrence évidente montre que :
.
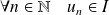Fondamental :
La suite
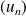est bien définie si la fonction
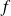est une fonction continue sur un intervalle
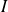de
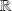et si :
.
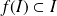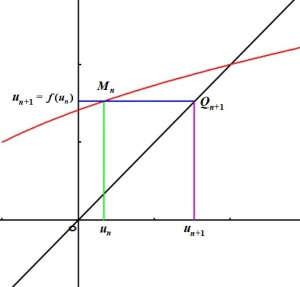
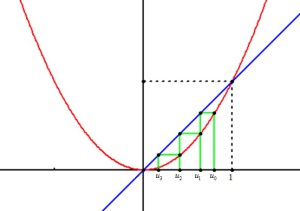
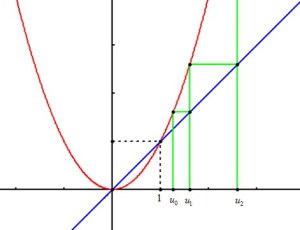
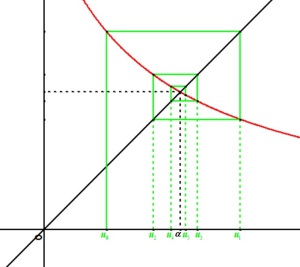
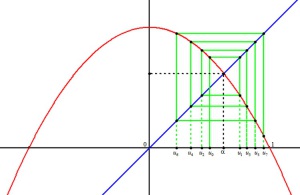
Fondamental : Construction géométrique
La construction suivante permet de visualiser la suite. Elle permet de formuler des conjectures que l'on démontre ensuite par récurrence. On trace la courbe représentative de
Si l'on place
La parallèle à l'axe des abscisses passant par
Elle coupe donc la première bissectrice en un point
Donc il suffit de projeter
Et l'on recommence la construction pour obtenir le terme suivant. De proche en proche, on peut ainsi représenter géométriquement tous les termes de la suite sur l'axe des abscisses et observer son comportement. |  |
Cas d'une fonction croissante
Par une récurrence évidente :
.
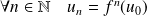Or, si
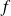est croissante sur
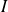, la fonction
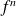est croissante sur
.
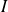Si
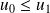, alors :
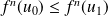, donc
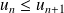. Donc la suite est croissante.Si
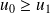, alors :
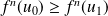, donc
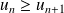. Donc la suite est décroissante.
Fondamental :
Lorsque la fonction
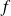est croissante sur
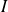, la suite
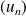est monotone.
C'est la comparaison de
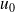et
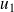qui détermine son sens de variations.
Exemple :
Par exemple, la fonction
:
est croissante sur
et vérifie :
.
Suivant les valeurs de
, on obtient soit une suite croissante, soit une suite décroissante.
Si
|  |
Si
|  |
Cas d'une fonction décroissante
Si
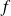est décroissante sur
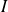, la fonction
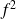est croissante sur
.
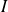La suite de terme général
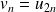est définie par :
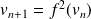, donc elle est monotone.
La suite de terme général
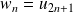est définie par :
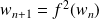, donc elle est monotone.
Si
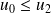, alors
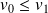, donc la suite
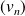est croissante.Mais
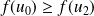, donc
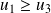, donc
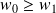, donc la suite
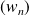est décroissante.
Si
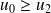, alors
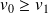, donc la suite
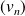est décroissante.Mais
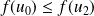, donc
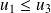, donc
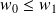, donc la suite
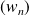est croissante.
Fondamental :
Lorsque la fonction
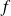est décroissante sur
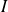, la suite
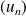n'est pas monotone, mais les suites extraites
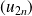et
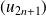sont monotones de sens contraires.
La suite
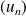est convergente si et seulement si ces suites
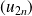et
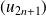convergent vers la même limite, donc sont adjacentes.
Exemple :
Par exemple, la fonction
Les deux suites sont adjacentes, donc la suite
|  |
Mais les deux suites ne sont pas toujours adjacentes.
Les termes de rangs pairs et impairs peuvent s'écarter au lieu de se rapprocher.
Exemple :
Par exemple, la fonction
Sur le graphique, la suite
Donc la suite
|  |
Calcul de la limite
On suppose que l'intervalle
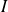est de la forme
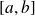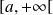ou
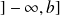ou
ou
.
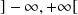On suppose que la suite
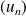converge vers une limite
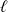. Donc :
.
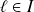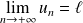, donc par continuité de
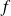sur
:
.
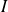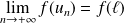Donc, par unicité de la limite de la suite :
.
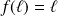Fondamental :
On suppose que l'intervalle
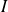est de la forme
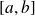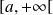ou
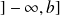ou
ou
.
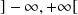Si la suite
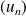est convergente, sa limite est solution de l'équation :
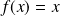dans
.
Résoudre cette équation permet de déterminer les seules limites possibles de la suite.
Conformément à l'étude graphique, ce sont les abscisses des points d'intersection de la courbe avec la première bissectrice.
Si l'équation
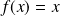n'a pas de solution dans I, cela prouve que la suite
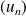est divergente.
Si l'équation
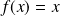admet plusieurs solutions dans
, des inégalités sur
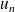peuvent permettre d'affiner la recherche et d'éliminer certaines solutions.
Lorsque l'on a déterminé une solution
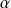, dans certains cas, l'inégalité des accroissements finis peut permettre d'étudier la convergence de la suite.
En effet, supposons que
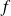est dérivable sur
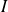et que :
.
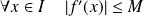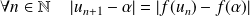, donc :
.
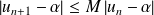Donc :
.
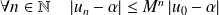Donc si
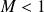, la suite
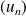converge vers
.
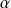