Eléments propres d'une matrice carrée
Dans ce qui suit,
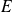désigne un espace vectoriel de dimension
.
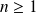Fondamental :
Un scalaire
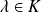est valeur propre d'une matrice carrée
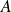de
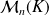si la matrice
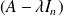n'est pas inversible, donc si :
.
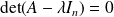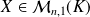est vecteur propre de la matrice
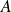associé à la valeur propre
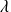si :
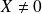et
.
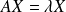Définition :
Le polynôme caractéristique d'une matrice
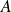de
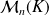est le polynôme :
.
Donc les valeurs propres de la matrice
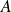sont les racines de son polynôme caractéristique.
Fondamental :
Propriété : Si un endomorphisme
a pour matrice
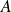dans une base de
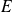, les valeurs propres de
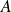sont les valeurs propres de l'endomorphisme
, et les vecteurs propres de
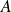sont les matrices des vecteurs propres de
dans la base considérée.
Conséquence : Deux matrices semblables ont les mêmes valeurs propres et le même polynôme caractéristique.
Le polynôme caractéristique de la matrice dépend donc de l'endomorphisme, et pas de la base considérée.
