Formes linéaires
Dans ce qui suit,
désigne un
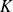- espace vectoriel.
Définition :
Une forme linéaire sur
est une application linéaire de
dans
.
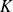L'ensemble
des formes linéaires sur
est appelé espace dual de
.
Par exemple, l'application qui à toute matrice de
associe sa trace est une forme linéaire.
Définition :
Si
est une base de
, la famille
définie par
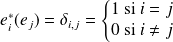est une base de
appelée base duale de
.
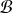La base
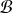est appelée base préduale de la base
.
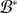Alors :
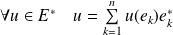. Et :
.
Rappel
Un hyperplan d'un espace vectoriel
de dimension
est un sous-espace vectoriel de
de dimension
.
Fondamental :
Propriétés :
Tout hyperplan de
est noyau d'une forme linéaire non nulle.Si
est une base de
, il admet une équation de la forme :
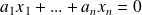.Un sous-espace vectoriel de
est de dimension
si et seulement si il est intersection de
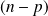hyperplans noyaux de formes linéaires indépendantes.
Par exemple, l'ensemble des matrices de
de trace nulle est un hyperplan de l'espace vectoriel
.
Fondamental :
L'ensemble
des solutions d'un système de
équations linéaires homogènes à
inconnues est intersection de
hyperplans de
.
Le rang du système est
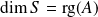où
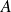est la matrice du système.
