Ondes dans une corde
Vibrations transversales d'une corde ; équation d'onde de d'Alembert
On considère une corde inextensible, de masse linéique
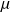 , tendue horizontalement avec une force constante
, tendue horizontalement avec une force constante
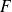 .
.
A l'équilibre, la corde est horizontale.
On supposera dans la suite que la pesanteur n'intervient pas (sinon, la forme de la corde serait une chaînette).
On se propose d'étudier les petits mouvements au voisinage de cet équilibre, avec le modèle suivant :
L'élément de corde situé au point de coordonnées
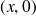 à l'équilibre se trouve au point de coordonnées
à l'équilibre se trouve au point de coordonnées
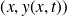 hors équilibre ; autrement dit, on néglige son déplacement le long de (Ox).
hors équilibre ; autrement dit, on néglige son déplacement le long de (Ox). L'angle
 que fait la tangente à la corde au point d'abscisse
que fait la tangente à la corde au point d'abscisse
 à l'instant
à l'instant
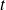 est un infiniment petit (
est un infiniment petit (
 ,
,
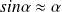 et
et
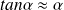 .
.Si on considère une coupure fictive au point d'abscisse
 , l'action exercée par la partie gauche de la corde sur la partie droite se réduit à une force tangente à la corde notée
, l'action exercée par la partie gauche de la corde sur la partie droite se réduit à une force tangente à la corde notée
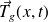 .
.De même, l'action exercée par la partie droite sur la partie gauche se réduit à une force
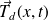 .
. D'après le principe des actions réciproques,
 .
.
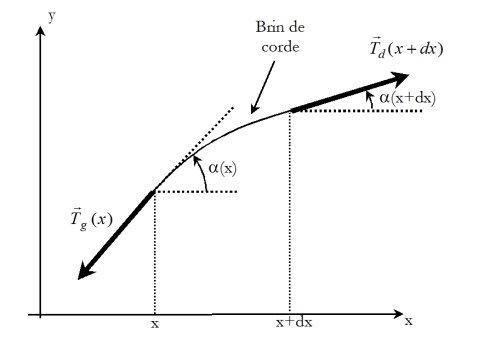
Le théorème du CI appliqué à un élément de corde situé entre les abscisses
 et
et
 donne :
donne :

En projection, et en notant
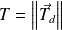 :
:
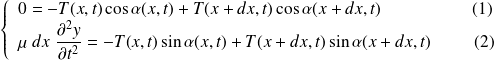
Si on se limite à l'ordre 1, l'équation (1) donne :
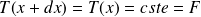
L'équation (2) se réécrit :
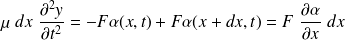
Or :
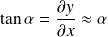
D'où :

On retrouve là encore l'équation d'ondes de d'Alembert.
Dans le cas de la corde, l'onde est dite transversale (le déplacement a lieu selon Oy).
Attention : Équation d'onde de d'Alembert

On retrouve une équation d'ondes de d'Alembert.
La vitesse de propagation de l'onde est :
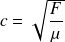
La vitesse est d'autant plus grande que la corde est tendue et que la corde est légère.
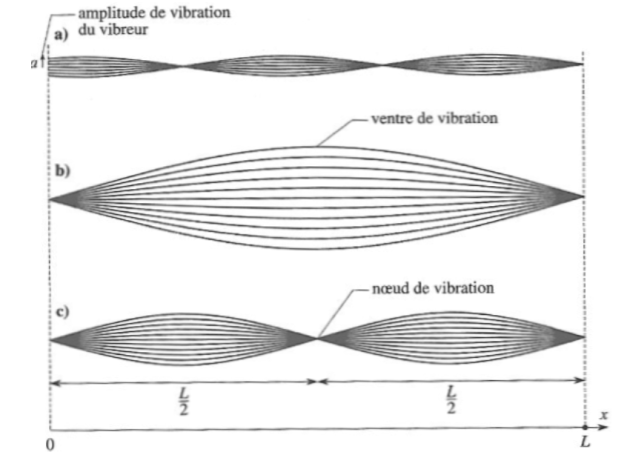
Exemple : Modes propres d'une corde vibrante fixée à ses deux bouts
Exemple : La corde de Melde
Dans l'expérience de Melde, l'extrémité d'abscisse
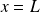 d'une corde est fixée (
d'une corde est fixée (
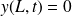 ) et un opérateur impose en
) et un opérateur impose en
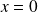 un déplacement harmonique :
un déplacement harmonique :
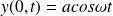
De pulsation
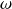 .
.
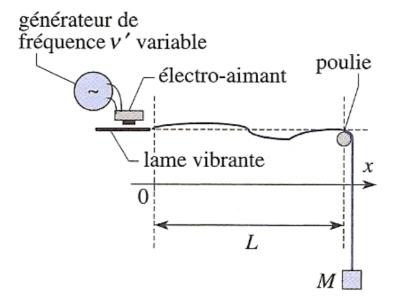
On s'intéresse au régime forcé, obtenu après disparition du régime transitoire.
On cherche ainsi une solution de l'équation de d'Alembert correspondant à une onde stationnaire de même pulsation que l'excitation :
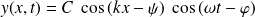
Les conditions aux limites imposent :
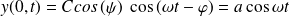
Et :
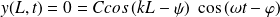
D'où :
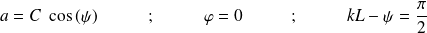
Soit :
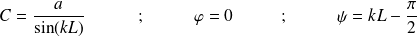
Par conséquent :
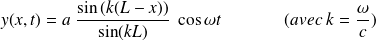
L'amplitude est maximale pour :
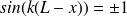
Et vaut, en valeur absolue :
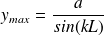
Cette amplitude maximale devient infinie (la corde est alors en résonance) pour des pulsations excitatrices telles que :
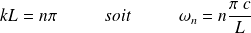
correspondant aux modes propres de la corde.
Néanmoins, d'inévitables amortissements et la raideur de la corde font que l'amplitude maximale garde une valeur finie.
Ainsi l'onde stationnaire devient résonante (en régime forcé) lorsque la pulsation d'excitation du vibreur coïncide avec une des pulsations propres (en régime libre) de vibration de la corde, exactement comme pour un circuit LC série où la pulsation
 désigne à la fois la pulsation propre en régime libre et la pulsation de résonance en régime forcé.
désigne à la fois la pulsation propre en régime libre et la pulsation de résonance en régime forcé.
Une vidéo sur la corde de Melde
Complément : Une vidéo (en anglais) sur les ondes mécaniques
Complément : Une vidéo de cours sur les ondes dans une corde
Simulation : Une animation JAVA de JJ.Rousseau (Université du Mans)
Simulation : Animation JAVA (University of Colorado Boulder)
Onde sur une corde :