Mouvements de particules chargées dans des champs électriques et magnétiques
Méthode : Champ électrique seul
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ électrostatique
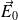uniforme et indépendant du temps.
Le référentiel d'étude est celui du laboratoire supposé galiléen.
Le PFD appliqué à la particule donne :
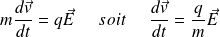
Il y analogie avec un point matériel dans le champ de pesanteur supposé uniforme :
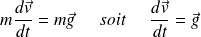
Par conséquent, le mouvement d'une particule dans le champ
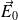sera soit une droite soit une parabole.
Méthode : Champ magnétique seul
Puissance de la force magnétique :
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ magnétostatique
uniforme et indépendant du temps.
Le référentiel d'étude est celui du laboratoire.
Le PFD appliqué à la particule donne :
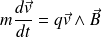
La puissance de la force magnétique est nulle (
).
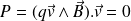Par conséquent, d'après le théorème de la puissance cinétique :
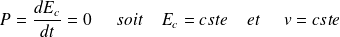
Un champ magnétique ne modifie pas la norme de la vitesse mais seulement sa direction.
Mouvement circulaire :
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ magnétostatique
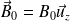uniforme et indépendant du temps.
La vitesse initiale de la particule est perpendiculaire au champ et portée, par exemple, selon l'axe (Ox) :
.
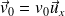Le PFD permet d'obtenir le rayon de la trajectoire (on suppose ici
) :
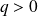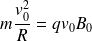
Soit :
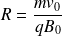
Ce cercle est parcouru à la vitesse angulaire constante :
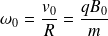
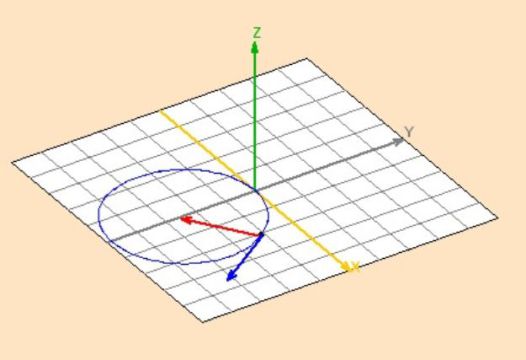
Mouvement hélicoïdal :
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ magnétostatique
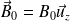uniforme et indépendant du temps.
La vitesse initiale de la particule est quelconque et peut s'écrire, par un choix convenable des axes :
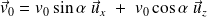
La trajectoire dans le plan perpendiculaire à l'axe (Oz) est un cercle de rayon :
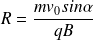
parcouru à la vitesse angulaire
.
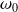Le mouvement est rectiligne uniforme selon l'axe (Oz), à la vitesse
.
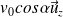La trajectoire est une hélice dont le pas est constant. Ce pas
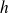vaut (c'est la distance parcourue pendant une période du mouvement circulaire dans le plan (Oxy)) :
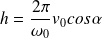
Des vidéos illustrant divers mouvements :
Méthode : Champ électrique et champ magnétique
Hélice à pas variable :
On considère une particule chargée ponctuelle M (+ q) de masse m en mouvement dans un champ magnétostatique
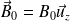uniforme et indépendant du temps et dans un champ électrique
.
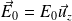La vitesse initiale de la particule est quelconque et peut s'écrire, par un choix convenable des axes :
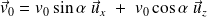
Le mouvement selon l'axe (Oz) est désormais accéléré :
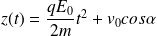
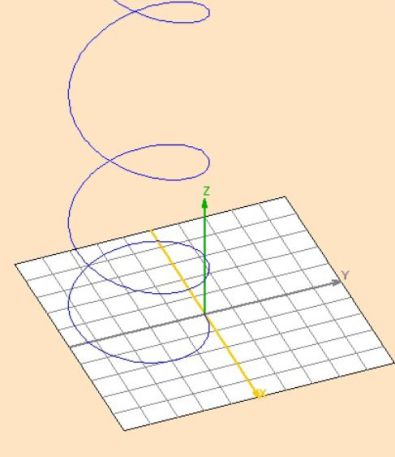
Cycloïde :
On considère une particule chargée ponctuelle M (+ q > 0) de masse m en mouvement dans un champ magnétostatique
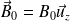uniforme et indépendant du temps et dans un champ électrique
.
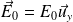La particule est initialement à l'origine O du repère et sa vitesse initiale est nulle.
On posera :
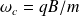
Montrer que les équations paramétriques de la trajectoire sont :
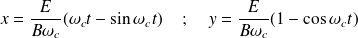
Une animation Java sur un filtre de vitesse et la mesure du rapport e / m :
Une vidéo illustrant le mouvement d'une particule dans des champs électrique et magnétique croisés :
