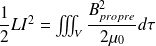Énergie magnétique d'un système de deux circuits
Définition : Loi d'Ohm généralisée
On considère deux circuits filiformes (C1) et (C2) en couplage mutuel.
Alors, en l'absence d'autres sources de champs magnétiques :
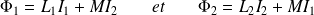
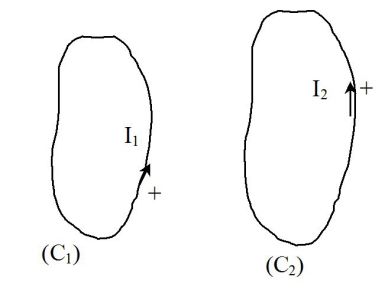
Si les circuits sont rigides et immobiles dans le référentiel du laboratoire, les fém d'induction valent :
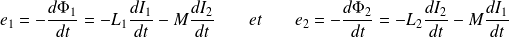
La ddp aux bornes de chaque circuit est alors :
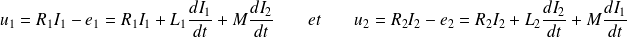
Définition : Énergie magnétique d'un système de deux circuits
La puissance électrique reçue par les deux circuits vaut :
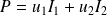
Soit :
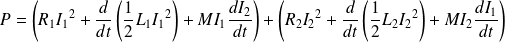
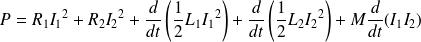
Finalement :
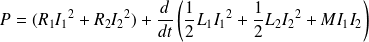
On reconnaît d'une part la puissance dissipée par effet Joule et on définit d'autre part :
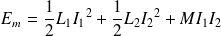
Comme étant l'énergie magnétique du système des deux circuits, en l'absence d'autres sources de champs magnétiques et en prenant comme convention que cette énergie est nulle lorsque les courants sont nuls.
Attention : Énergie magnétique du système des deux circuits
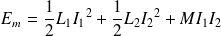
Remarque : Couplage idéal
On peut montrer que :
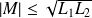
On pose :
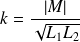
le coefficient de couplage entre les deux circuits. Ce coefficient est compris entre 0 et 1.
Le cas limite k = 1, soit
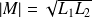 , correspond au cas où toutes les lignes de champ du champ magnétique créé par un des deux circuits traversent l'autre circuit. Il s'agit du cas idéal du couplage parfait.
, correspond au cas où toutes les lignes de champ du champ magnétique créé par un des deux circuits traversent l'autre circuit. Il s'agit du cas idéal du couplage parfait.
Exemple : Exercice sur les circuits couplés
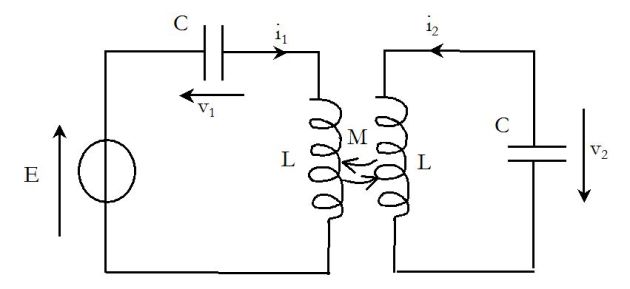
On considère désormais le circuit suivant :
Les tensions et les intensités sont reliées :
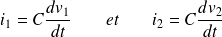
La loi des mailles donne :
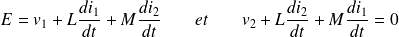
D'où :
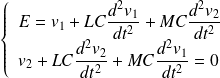
Recherche des modes propres
On suppose que E = 0 (régime libre).
On cherche des solutions harmoniques de même pulsation
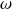 .
.
Alors :
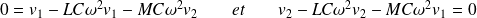
D'où le système homogène :
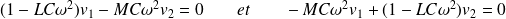
Ce système possède une solution non triviale si son déterminant est nul :
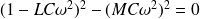
Soit :
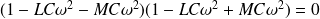
On en déduit les deux pulsations propres (avec
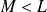 ) :
) :
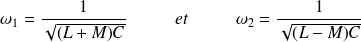
Pour le 1er mode propre,
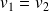 : les deux tensions oscillent en phase.
: les deux tensions oscillent en phase.
Pour le 2nd mode propre,
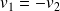 : les deux tensions oscillent en opposition de phase.
: les deux tensions oscillent en opposition de phase.
Le régime libre correspond à une superposition linéaire de ces deux modes propres.
Remarque : Autre définition de l'inductance propre d'un circuit
On considère un circuit (filiforme ou non) sans interaction mutuelle avec un autre circuit.
Pour étendre la définition de
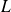 , on peut identifier les deux expressions de l'énergie magnétique, soit :
, on peut identifier les deux expressions de l'énergie magnétique, soit :