Le modèle de Bohr
Les postulats de Bohr
L'atome d'hydrogène est constitué d'un proton O (de masse M et de charge électrique +e) et d'un électron P (de masse m<<M et de charge –e) qui décrit une orbite circulaire de rayon r autour du proton.
Le proton est supposé fixe et est l'origine d'un référentiel galiléen (celui du laboratoire).
La seule force prise en compte ici est la force d'interaction coulombienne entre les deux charges.
Les postulats de Bohr sont :
Il existe des orbites stables (nommées orbites stationnaires) pour lesquelles l'électron ne rayonne aucune énergie.
L'électron ne rayonne ou n'absorbe de l'énergie que lors du passage d'une orbite stationnaire à une autre.
Comment caractériser les orbites stationnaires ?
Bohr montra qu'au travers des conditions imposées par ses postulats, les orbites stationnaires étaient celles pour lesquelles le moment cinétique de l'électron était un multiple entier d'une constante notée
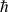, qui vaut
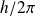, où
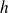est la constante de Planck.
Ainsi, si
est le moment cinétique de l'électron par rapport au proton sur une orbite stationnaire, alors :
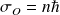
où n est un entier positif.
Méthode : Une étude mécanique
On va déterminer une relation entre le rayon
de la trajectoire et la vitesse
de l'électron.
La relation fondamentale de la dynamique, appliquée à l'électron dans le référentiel galiléen lié au noyau, donne, en projection sur le rayon OP :
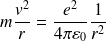
Soit :
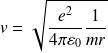
On peut exprimer l'énergie cinétique
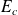, l'énergie potentielle
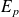puis l'énergie mécanique
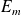de l'électron en fonction de
et des constantes
et
:
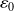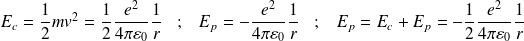
Fondamental : La quantification du moment cinétique, des rayons et des énergies de l'atome
Pour interpréter les raies spectrales de l'atome d'hydrogène, le modèle de Bohr impose à l'électron un moment cinétique quantifié :
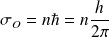
où
est un entier naturel non nul et
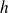la constante de Planck.
On va déterminer les rayons, notés
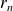, des orbites permises.
Le moment cinétique de l'électron par rapport au noyau situé en O s'écrit :
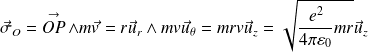
La condition de quantification du moment cinétique imposée par N.Bohr entraîne une quantification des rayons (notés désormais
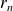) des orbites permises. En effet, l'expression :
donne :
où
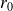désigne le rayon de l'orbite de l'électron pour
.
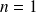L'état de l'électron associé à
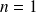est appelé état fondamental et
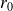est appelé rayon de Bohr.
On peut montrer que l'énergie de l'électron est quantifiée et peut s'écrire :
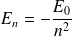
En effet :
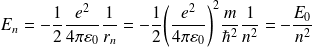
Avec :
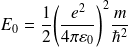
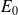représente l'énergie mécanique de l'électron dans l'état fondamental.
Numériquement :
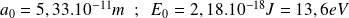
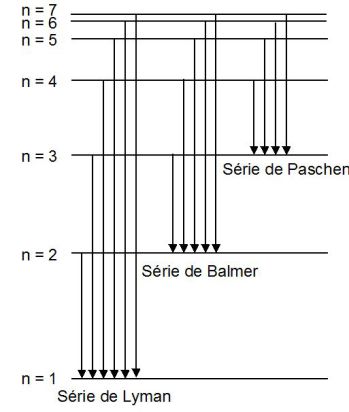
Exemple : La série de Balmer
En réalisant une décharge électrique dans une ampoule remplie de dihydrogène, les molécules de dihydrogène se dissocient et les atomes excités émettent des rayonnements électromagnétiques de différentes longueurs d'onde.
Le physicien J. Balmer détermina expérimentalement que les longueurs d'onde
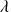de ces rayonnements, situés dans le domaine de la lumière visible, vérifiaient la relation phénoménologique suivante : (avec
entier positif)
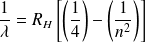
Où
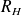est la constante de Rydberg, qui vaut
.
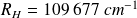Le modèle de Bohr permet de déterminer la valeur théorique attendue pour cette constante
:
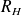Lorsque l'atome d'hydrogène passe d'un niveau défini par le nombre quantique n à l'état correspondant au nombre quantique 2, il émet un photon dont l'énergie est donnée par :
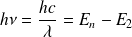
Par conséquent, le nombre d'onde (défini comme l'inverse de la longueur d'onde du rayonnement émis) s'écrit :
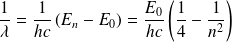
La constante de Rydberg s'interprète donc comme la quantité :
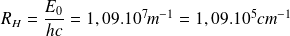
dont la valeur théorique est en très bon accord avec la valeur expérimentale déterminée par J.Balmer.
En conclusion, le modèle de Bohr donne les bons niveaux d'énergie pour l'atome d'hydrogène.
En revanche, la représentation classique d'un électron se mouvant sur une orbite circulaire autour du proton a été mise à défaut par la mécanique quantique.
Cette dernière nous renvoie l'image d'un électron délocalisé dont on ne peut connaître que la probabilité de présence, « matérialisée » par un nuage de probabilité (les orbitales atomiques) entourant le noyau.
Exemple : Le positronium
Le modèle de Bohr peut être appliqué au positronium, système qui est constitué d'un électron (de masse
et de charge
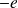) et d'un positron (l'antiparticule de l'électron, de même masse
mais de charge
) en rotation l'un par rapport à l'autre.
Le positronium ne constitue pas un système stable ; il se désintègre principalement en deux photons
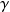selon le schéma :
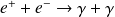
La durée de vie du positronium (définie comme la durée nécessaire pour que, parmi
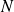positroniums,
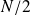se soient annihilés) est de l'ordre de
.
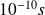L'étude du positronium peut se ramener à l'étude d'une particule fictive
.
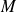Le système à deux corps constitué de l'électron et de son antiparticule, peut se ramener à l'étude d'une particule fictive M, de masse égale à
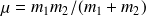, masse réduite du système, tournant autour du centre d'inertie G des deux particules à une distance égale à :
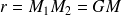
où
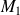et
sont les positions de l'électron et du positron.
Le référentiel d'étude, lié au centre d'inertie du système, est galiléen puisque le positronium est supposé isolé.
On peut évaluer l'énergie de liaison du positronium dans son état fondamental ainsi que le rayon de son orbite fondamentale.
Le principe fondamental de la dynamique, appliqué à la particule fictive dans le cas d'une trajectoire circulaire, donne en projection sur la droite GM :
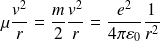
L'énergie mécanique du positronium, égale à celle de la particule fictive, vaut :
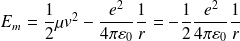
Le moment cinétique du positronium, égal à celui de la particule fictive par rapport à G, s'écrit :
Par analogie avec l'atome d'hydrogène, le modèle de Bohr appliqué au positronium conduira aux mêmes résultats, à condition de remplacer la masse de l'électron par la masse réduite du positronium, soit m/2.
L'énergie du niveau fondamental du positronium est donc :
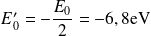
Et l'énergie de liaison :
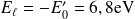
Le rayon de l'orbite fondamentale s'écrit :
