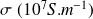Local Ohm's law
Fondamental : Drude model presentation (1900)
In a metallic (“ohmic”) conductor under an electric voltage, the carrier electrons begin to move.
Intensity
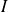 of electric current and current density vector
of electric current and current density vector
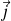 are defined by :
are defined by :
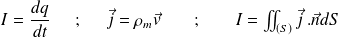
With :
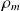 : density of mobile charges (
: density of mobile charges (
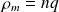 , where
, where
 is the density of mobile charges).
is the density of mobile charges).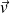 : the velocity of
: the velocity of
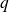 charge carriers.
charge carriers.
Let
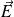 be the electric field responsible for the motion of mobile charges.
be the electric field responsible for the motion of mobile charges.
A mobile charge undergoes an electric force :
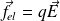
It also undergoes a force due to stationary charges which compose the crystal lattice of the metallic conductor.
This force can be modeled.
We model it by a fluid friction :
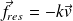
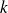 is a phenomenological constant which depends on the metallic conductor studied.
is a phenomenological constant which depends on the metallic conductor studied.
Fondamental : Fundamentals : ohm's local law and conductivity of a metallic conductor
Newton's second law applied to a mobile charge in the laboratory referential gives : (
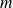 is the mass of a charge carrier)
is the mass of a charge carrier)
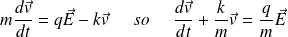
Let
 be defined by :
be defined by :
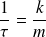
 is the relaxation time of the ohmic environment.
is the relaxation time of the ohmic environment.
The differential equation becomes :
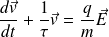
Suppose the electric field does not depend on time.
The solution to this equation is :
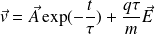
In a steady-state (for
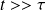 ) :
) :
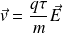
The current density vector can be deduced :
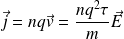
Let
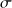 , the electric conductivity of the environment be defined by :
, the electric conductivity of the environment be defined by :
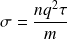
Attention : Ohm's local law
For a conductor whose conductivity is
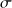 (For a conductor whose conductivity is
(For a conductor whose conductivity is
 ) :
) :
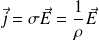
The limitation of the carriers migration speed explains Ohm's local law.
The interactions with the matter of the medium (the stationary cations of the metallic grid) slow the charge carriers down.
Order of magnitude :
The charge carriers are electrons.
The following table shows the conductivity of several usual metals at room temperature (300 K) :
Métaux | Ag | Cu | Au | Al | Hg |
| 6,21 | 5,88 | 4,55 | 3,65 | 0,10 |
We can evaluate the relaxation time for copper :
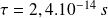
The steady-state is rapidly reached.
At least as long as the characteristic duration of field
 variations are greatly superior to
variations are greatly superior to
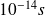 .
.
Thus, Ohm's local law remains true as long as the frequencies of the electric field are not too high (it is called low-frequency approximation).
Complément : Electric resistance and macroscopic Ohm's Law
Let's consider a cylindrical metallic conductor which has a transverse section
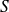 and a length
and a length
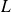 (for instance an electric copper cable).
(for instance an electric copper cable).
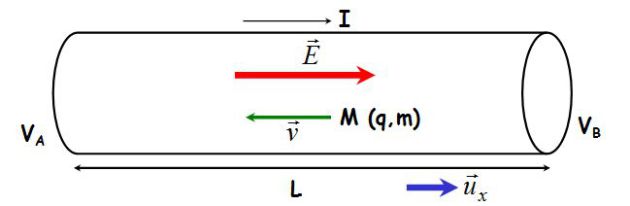
The field inside the wire is (in a steady-state regime) :
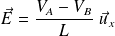
According to Ohm's local law :
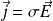
However :
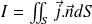
Thus :
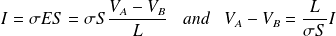
Let
 :
:
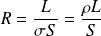
be the electrical resistance of the wire.
Then (in receiver convention) :
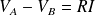
It is the macroscopic Ohm's Law.