Power of the induced electromotive force and the Laplace's force
Fondamental :
A charge carrier is put in a permanent magnetic field.
It moves with a velocity
in relation to the conductor, but the conductor moves at velocity
in the laboratory referential
.
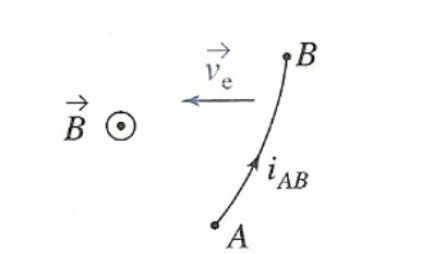
In this referential, the charge carrier has a speed (
) and is subject to Lorentz's Force :
Yet its power is equal to zero :
This power can be separated in 4 terms, and two of them are equal to zero :
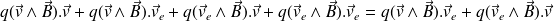
In an elementary volume
, the number of charge carriers is
.
The density of power of Lorentz's force is :
The term :
represents the density of power of the force applied to the charges because of the electromotive field
.
This density is evaluated in the referential of the conductor.
By adding it on the whole volume of the conductor, the power of the induced electromotive force
is found :
Interpretation of the term
:
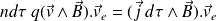
This term appears to be the power of Laplace's force applied to elementary volume
.
Finally, after integration :
The power of the induction electromotive force is compensated by that of the actions of the Laplace's force on the circuit.
Attention : Power of induced electromotive force and Laplace's force
The power of the induction electromotive force is compensated by that of the actions of the Laplace force on the circuit.
